Hydrodynamic Stability
Many intriguing and important fluid dynamic phenomena in nature and engineering are associated with complex spatio-temporal patterns, e.g. clouds, water waves, sprays, turbulent flows (Fig 1. shows wind driven waves on the surfce of a long puddle of water). This complexity arises from the nonlinear feedback and coupling inherent in the Navier-Stokes and accompanying scalar-transport partial differential equations. A first step towards decoding this complexity is to understand how spatio-temporal patterns arise from simpler steady and homogeneous states, namely the study of hydrodynamic stability. This field was pioneered by the great fluid dynamicists, including Rayleigh, Kelvin, Helmholtz and Taylor. The formation of waves/vortices between fluid layers travelling at different speeds is termed the “Kelvin-Helmholtz” instability; breakup of liquid jets into droplets due to surface tension is the “Rayleigh-Plateau” instability; the spontaneous toppling over of a layer of heavy fluid placed on top of a lighter one is the “Rayleigh-Taylor” instability. Hydrodynamic stability also plays a key role in understanding the transition from laminar flow to turbulent flow – a field that was born with the now famous study by Reynolds of flow transition in a tubular channel. The simplest approach to studying stability of a flow is to analyse how the system responds to small disturbances, i.e. via a “Linear stability analysis”. This theory helps to identify the critical threshold beyond which the flow becomes unstable, and also sheds light on the spatio-temporal pattern that emerges post instability. Our recent work in this area has focused on the stability of layered multiphase flows in microchannels. This work is relevant to the formation of drops and compound drops from annular confined jets (Fig. 2) [1], the transition from layered to slug flow, and the enhancement of inter-phase mass transfer via Marangoni stresses or centrifugal forces [2]-[3]. More recently, we have begun working on the stability of flow in flexible-wall channels. The instability characteristics change completely when the channel walls are soft, due to a two-way elastohydrodynamic coupling between the fluid and the soft-gel wall. Such situations arise in PDMS based microchannels and biological conduits, such as blood capillaries and mucus lined pulmonary airways.

Fig. 1: Wind driven waves on the surface of a long puddle of water. The flat-surface base state is unstable under strong wind forcing and gives rise to an array of relatively well ordered waves and move in the direction of the wind.
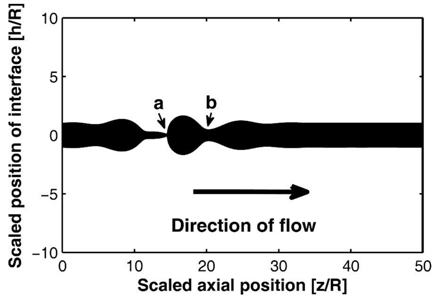
Fig. 2:Jet break up phenomena. Interface profile at the time of pinch-off (spatial analysis).
Analytical Modeling :
Mathematical modeling may be considered to be an art as well as a science (R. Aris, Mathematical Modelling Techniques, 1978).
Just as an artist's creative freedom can often prove to be the strongest credit to his work, so too in modelling, a modeller has the
freedom to choose the level of complexity, among other things, based on the objective of the modelling exercise. Although there are
several reasons to model (J. Epstein, Why Model, JASS, 2008), two of the primary goals are to predict a system behaviour and to
explain/understand a phenomenon. When it comes to accurate predictions, one is often left with no choice but to add in so much detail
so as to render the model unsolvable except by the use of numerical techniques and powerful computers. While such simulations have been
of great benefit to science and especially engineering, they are not the best place to look for insight and understanding. Instead, a
simplified model which is amenable to analytical solution may lead to a clearer explication of the underlying physics.
Our lab works on several studies of a fundamental nature. In these cases we employ simple mathematical models to answer the why,
how and what if questions about new phenomena in fluid flow, transport and reactive systems. Apart from studying purely linear models we
also study nonlinear systems by employing analytical methods such as asymptotic expansions and linear stability analysis.
References:
[1] D. S. Pillai, J. R. Picardo, and S. Pushpavanam, “Shifting and breakup instabilities of squeezed elliptic jets,” Int. J. Multiph. Flow, vol. 67, pp. 189–199, 2014.
[2] J. R. Picardo, T. G. Radhakrishna, and S. Pushpavanam, “Solutal Marangoni instability in layered two-phase flows,” J. Fluid Mech., vol. 793, no. 2016, pp. 280–315, 2016.
[3] J. R. Picardo, P. Garg, and S. Pushpavanam, “Centrifugal instability of stratified two-phase flow in a curved channel,” Phys. Fluids, vol. 27, no. 5, 2015.

