Our research focuses on developing new materials and technologies for energy conversion and storage. We explore novel approaches to renewable energy systems, battery technologies, and advanced materials with unique properties.
Learn More
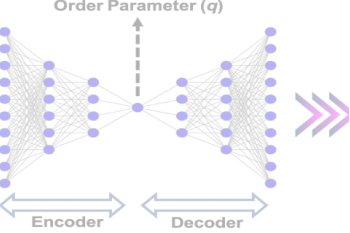
We employ advanced computational techniques to model and simulate molecular systems. Our work helps predict material properties, understand chemical reactions, and design new molecules with desired characteristics.
Learn More
Our group develops methodologies for the design, operation, and control of chemical processes. We integrate process modeling, optimization, and control strategies to improve efficiency and sustainability in chemical manufacturing.
Learn More
We investigate novel technologies and methodologies to dramatically improve process efficiency. Our work includes developing compact, energy-efficient equipment and innovative process designs that reduce environmental impact.
Learn More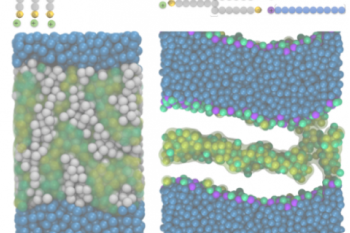
Our research addresses critical environmental issues including pollution control, waste treatment, and sustainable resource management. We develop technologies to minimize industrial environmental impact and promote circular economy principles.
Learn More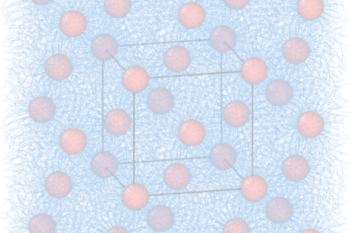
We study the fundamental aspects of chemical reactions and their engineering applications. Our work includes catalyst development, reactor design, and optimization of reaction conditions for industrial applications.
Learn More